最短路径算法

Start

  最短路问题也属于图论算法之一，解决的是在一张有向图当中点与点之间的最短距离问题。最短路算法有很多，比较常用的有bellman-ford、dijkstra、floyd、spfa等等。这些算法当中主要可以分成两个分支，其中一个是
bellman-ford及其衍生出来的spfa，另外一个分支是dijkstra以及其优化版本。floyd复杂度比较高，一般不太常用。
  这次就先简单说一下bellman-ford和SPFA算法。

First

存图

我们要对一张有向图计算最短路，那么我们首先要做的就是将一张图存储下来。关于图的存储的数据结构，常用的方法有很多种。最简单的是邻接矩阵，所谓的邻接矩阵就是用一个二维矩阵存储每两个点之间的距离。如果两个点之间没有边相连，那么设为无穷大。

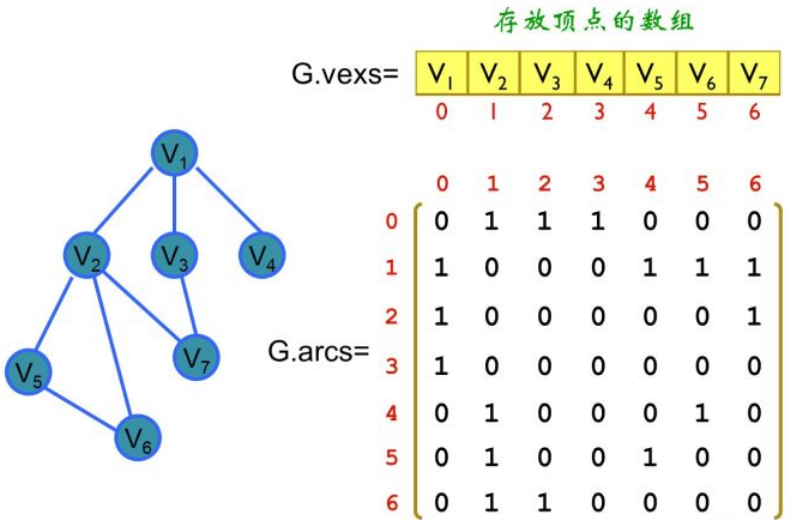
  这种方法的好处就是非常直观，实现也很简单，但是这中方法所消耗的时间复杂度也是很高的 $V^2$,这里的V指的是顶点的数量当顶点的数量稍稍大一些之后，带来的开销是非常庞大的。一般情况下我们的图的边的密集程度是不高
的，也就是说大量点和点之间没有边相连，我们浪费了很多空间。一般情况下当边是顶点的10倍时(也就是稠密图)我们选择这种存图方式,此外我们就选择邻接表的方式来存储稀疏图

  所谓的邻接表也就是说我们把顶点一字排开存入数组当中，每个顶点对应一条链表。这条链表当中存储了这个点可以到达的其他点的信息。邻接表的好处是可以最大化利用空间，有多少条边存储多少信息。但是也有缺点，除了实现稍稍复
杂一点之外，另外一个明显的缺点就是我们没办法直接判断两点之间是否有边存在，必须要遍历链表才可以。除了邻接矩阵和邻接表之外，还有一些其他的数据结构可以完成图的存储。比如前向星、边集数组、链式前向星等等。这些数据结构并没有
比邻接表有质的突破，对于非算法竞赛同学来说，能够熟练用好邻接表也就足够了。

bellman-ford算法

  刚才上面描述当中提到的算法除了floyd算法是计算的所有点对之间的最短距离之外，其他算法解决的都是单源点最短路的问题。所谓的单源点可以简单理解成单个的出发点，也就是说我们求的是从图上的一个点出发去往其他每个点的最短
距离。既然如此，我们的出发点以及到达点都是确定的，不确定的只是它们之间的距离而已。

  为什么我们会将bellman-ford算法和dijkstra算法区分开呢？因为两者的底层逻辑是不同的，bellman-ford算法的底层逻辑是动态规划， 而dijkstra算法的底层逻辑是贪心。

  bellman-ford算法的得名也和人有关，我们之前在介绍KMP算法的时候曾经说过。由于英文表意能力不强，所以很多算法和公式都是以人名来取名。bellman-ford是Richard Bellman 和 Lester Ford 分别发表的，实际上还有一个
叫Edward F. Moore也发表了这个算法，所以有的地方会称为是Bellman-Ford-Moore 算法。

  算法的原理非常简单，利用了动态规划的思想来维护源点出发到各个点的最短距离。

  它的核心思维是松弛，所谓的松弛可以理解成找到了更短的路径对原路径进行更新。对于一个有V个节点的有向图进行V-1轮松弛，从而找到源点到所有点的最短距离。

  初始的时候我们会用一个数组记录源点到其他所有点的距离，对于与源点直接相连的点来说，这个距离就是它和源点的距离否则则是无穷大。对于第一轮松弛来说，我们寻找的是源点出发经过一个点到达其他点的最短距离。我们用s代表源
点，我们寻找的就是s经过点a到达点b，使得距离小于s直接到b的距离。

  第二轮松弛就是寻找的s经过两个点到达第三个点的最短距离，同理，对于一个有V个点的图来说，两个点之间最多经过V-1个点，所以我们需要V-1轮松弛操作。

for (var i = 0; i < n - 1; i++) {
    for (var j = 0; j < m; j++) {//对m条边进行循环
      var edge = edges[j];
      // 松弛操作
      if (distance[edge.to] > distance[edge.from] + edge.weight ){ 
        distance[edge.to] = distance[edge.from] + edge.weight;
      }
    }
}

  Bellman-ford的算法很好理解，实现也不难，但是它有一个缺点就是复杂度很高。我们前面说了一共需要V-1轮松弛，每一轮松弛我们都需要遍历E条边，所以整体的复杂度是$O(VE)$，E指的是边的数量。想想看，假设对于一个有1w个顶点，10w条边的
图来说，这个算法是显然无法得出结果的。

  所以为了提高算法的可用性，我们必须对这个算法进行优化。我们来分析一下复杂度巨大的原因，主要在两个地方，一个地方是我们松弛了V-1次，另外一个地方是我们枚举了所有的边。松弛V-1次是不可避免的，因为可能存在极端的情况需要V-1次松弛
才可以达成。但我们每次都枚举了所有的边感觉有点浪费，因为其中大部分的边是不可能达成新的松弛的。那有没有办法我们筛选出来可能构成新的松弛的边呢？

  针对这个问题的思考和优化引出了新的算法——spfa。

SPFA算法

  SPFA算法的英文全称是Shortest Path Faster Algorithm，从名字上我们就看得出来这个算法的最大特点就是快。它比Bellman-ford要快上许多倍，它的复杂度是$O(kE)$，这里的k是一个小于等于2的常数。

  SPFA的核心原理和Bellman-ford算法是一样的，也是对点的松弛。只不过它优化了复杂度，优化的方法也很简单，用一个队列维护了可能存在新的松弛的点。这样我们每次从这些点出发去寻找其他可以松弛的点加入队列，这里面的原理
很简单，只有被松弛过的点才有可能去松弛其他的点。

  SPFA的代码也很短，实现起来难度很低，单单从代码上来看和普通的宽搜区别并不大。

Python版本：

import sys
from queue import Queue
que = Queue()

# 邻接表存储边
edges = [[]]
# 维护是否在队列当中
visited = [False for _ in range(V)]
dis = [sys.maxsize for _ in range(V)]
dis[s] = 0

que.put(s)
visited[s] = True

while not que.emtpy():
    u = que.get()
    for v, l in edges[u]:
        if dis[u] + l < dis[v]:
            dis[v] = dis[u] + l
            if not visited[v]:
                que.add(v)
                visited[v] = True
                
    visited[u] = False

参考题目

C++版本：

#include <queue>
#include <cstdio>
#include <cstring>
using namespace std;

const int N = 100010;

int n, m;
int h[N], e[N], ne[N], w[N], idx;
int dis[N];
bool st[N];

void add(int a, int b, int c) {
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++;
}

int spfa() {
    queue<int> q;
    q.push(1);
    memset(dis, 0x3f, sizeof dis);
    dis[1] = 0;
    st[1] = true;
    
    while ( !q.empty() ) {
        int t = q.front();
        q.pop();
        
        st[t] = false;
        
        for (int i = h[t]; i != -1; i = ne[i]) {
            int j = e[i];
            
            if (dis[j] > dis[t] + w[i]) {
                dis[j] = dis[t] + w[i];
                st[j] = true;
                q.push(j);
            }
        }
    }
    
    if (dis[n] == 0x3f3f3f3f) return -1;
    else return dis[n];
    
}

int main() {
    scanf("%d%d", &n, &m);
    memset(h, -1, sizeof h);
    
    while ( m -- ) {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c);
    }
    
    int t = spfa();
    
    if (t == -1) puts("impossible");
    else printf("%d", t);
}

Python版；

n, m, k = map(int, input().split())

## 用一个list 记录所有边的信息即可
g = []
dist = [float("inf") for i in range(n+1)]

for i in range(m):
    a, b, w = map(int, input().split())
    g.append([a, b, w])

def bellman_ford():
    dist[1] = 0

    ## 循环几次代表最多用几条边
    for _ in range(k):
        ## 必须backup 防止在过程中会更新dist里面的数据导致并不是最多k条边
        backup = dist[:]
        for i in range(m):
            a, b, w = g[i][0], g[i][1], g[i][2]
            dist[b] = min(dist[b], backup[a] + w)

bellman_ford()
print(dist[n] if dist[n] != float("inf") else "impossible")